Assalamualaikum semuanya perkenalkan nama saya Raihan Fallah Suryabima saya biasa dipanggil Raihan, saya berasal dari SMAN 63 Jakarta Selatan. Pada kesempatan kali ini saya akan memberikan contoh soal-soal dari materi vektor beserta pembahasannya. Soal yang saya berikan berasal dari refrensi google dan buku sekolah. Selamat belajar!!!
1. Menyelesaikan pengertian vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
1) Pengertian dari vektor berdimensi dua dan tiga
= Dalam vektor ruang dua dimensi  memiliki dua vektor basis yaitu
memiliki dua vektor basis yaitu  dan
dan 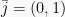 . Sedangkan dalam tiga dimensi
. Sedangkan dalam tiga dimensi  memiliki tiga vektor basis yaitu
memiliki tiga vektor basis yaitu 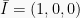 ,
, 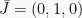 , dan
, dan  .
.

2) Pengurangan vektor berdimensi tiga
=



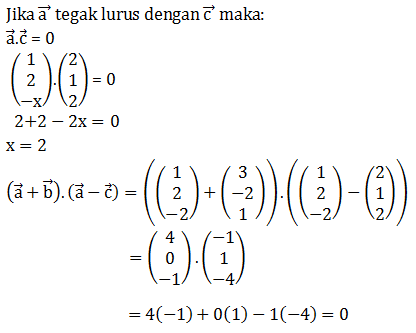
Pembahasan : {a} - {b} = {b} - {a}
= q - p = (2,5,-3)- (2,3,1)= (0,2,-4)
= r - q = (-3,1,2)- (2,5,-3)= (-5,-4,5)
2. Menyelesaikan operasi pertambahan (+) vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
1) Penjumlahan vektor berdimensi dua
=
2) Penjumlahan vektor berdimensi tiga
=

3. Menyelesaikan operasi pengurangan (-) vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
1) Pengurangan vektor berdimensi dua
=
2) Pengurangan vektor berdimensi tiga
=

4. Menyelesaikan operasi perkalian ( . ) dengan skalar vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
1) Ruang berdimensi dua
=
2) Ruang berdimensi tiga
=
5. Menyelesaikan operasi perkalian ( . ) dua vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
1) Ruang berdimensi dua
=
2) Ruang berdimensi tiga
=
6. Menyelesaikan kesamaan dua vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal:

7. Menyelesaikan panjang vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
1) Ruang berdimensi dua
=
2) Ruang berdimensi tiga
=
8. Menyelesaikan perbandingan antar vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
9. Menyelesaikan panjang proyeksi vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=

10. Menyelesaikan proyeksi vektor orthogonal dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
11. Menyelesaikan sifat vektor yang segaris/sejajar dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
12. Menyelesaikan sifat vektor yang tegak lurus dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
13. Menyelesaikan sifat vektor jika 2 vektor yang sama dikalikan maka hasilnya kuadrat dari panjang vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
14. Menyelesaikan sifat vektor jika 2 vektor yang berbeda dikalikan maka berlaku hukum komutatif dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
= Titik P(2,3,1), Q(2,5,-3), R(-3,1,2) Tentukan Vektor (QR} dan {PQ}
Pembahasan : {a} - {b} = {b} - {a}
= q - p = (2,5,-3)- (2,3,1)= (0,2,-4)
= r - q = (-3,1,2)- (2,5,-3)= (-5,-4,5)
15. Menyelesaikan sifat vektor jika 3 vektor berlaku hukum distributif dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
= Diketahui vektor a = (-6, 5, -2), b = (-5, 4, -3), dan c = (8, -7, 0). Jika c = ma + nb, maka
m-n =??
PEMBAHASAN
⇔ (8, -7, 0) = m x (-6, 5, -2) + n x (-5, 4, -3)
⇔ (8, -7, 0) = (-6m, 5m, -2m) + (-5n, 4n, -3n)
-6m + (-5n) = 8 ... (1)
5m + 4n = -7 ... (2)
-2m - 3n = 0 ... (3)
Ketiga persamaan di atas membentuk sistem persamaan linear.
Persamaan (1) dan (3), kIta eliminasi m, diperoleh
-6m - 5n = 8 |x 1|
-2m - 3n = 0 |x 3|
-6m - 5n = 8
-6m - 9n = 0
__________-
⇔ -5n - (-9n) = 8
⇔ -5n + 9n = 8
⇔ 4n = 8
⇔ n = 2
Kita substitusikan n = 2 ke persamaan (2), diperoleh
5m + 4n = -7
⇔ 5m + 4 x 2 = -7
⇔ 5m + 8 = -7
⇔ 5m = -7 - 8
⇔ 5m = -15
⇔ m = -15/5
⇔ m = -3
m - n = -3 - 2 = -5.
Jadi, jika vektor a = (-6, 5, -2), b = (-5, 4, -3), dan c = (8, -7, 0), kemudian c = ma + nb, maka nilai m - n adalah -5.
16. Menyelesaikan vektor searah, berlawanan arah, identitas dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
1. 2Diberikan vektor a=(-2,x,5), b=(3,-1,2), dan c=(y,-2,x).Vektor a tegak lurus dengan b.sedangkan vektor b searah dengan c.Tentukan :
a. Nilai x dan y
b. Hasil operasi (a+b-c)
PEMBAHASAN:
• a T b :
a.b = 0
(-2 x 5) (3 -1 2) = 0
-6 - x + 10 = 0
-x + 4 = 0
x = 4
• b // c
k.b = c
2(3 -1 2) = (y -2 x)
(6 -2 4) = (y -2 x)
diperoleh,
y = 6 dan x = 4
...
a = (-2 4 5)
b = (3 -1 2)
c = (6 -2 4)
maka,
• a+b+c
= (-2 4 5)+(3 -1 2)-(6 -2 4)
= [(-2+3-6) (4-1-(-2) (5+2-4)]
= [-5 5 3]
2. Diketahui ada titik A(2,4,6), titik B(6,6,2), dan titik C(p,q,-6). Apabila titik A, B, dan C segaris maka tentukan nilai p + q
17. Menyelesaikan proyeksi vektor ortogonal dengan skalar dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
1. Dua vektor u = 2i + 3j + mk dan v = 4i - 4j + 2k membentuk sudut tumpul. Jika panjang proyeksi vektor u pada v adalah 2, maka nilai m adalah ...
PEMBAHASAN:u = [2, 3, m]
v = [4, -4, 2]
Misalkan vektor proyeksi u pada v adalah p, dengan panjangnya adalah |p| = 2
Dari persamaan nilai mutlak diatas, diperoleh
2m - 4 = 12 atau 2m - 4 = -12
2m = 16 atau 2m = -8
m = 8 atau m = -4
Karena u dan v membentuk sudut tumpul, maka
u ‧ v < 0 ⇔ 2m - 4 < 0 ⇔ m < 2
Jadi, nilai m yang memenuhi adalah m = -4
2. Diketahui 3 titik A(4, -1, 2), B(4, 3, -2) dan C(1, 3, 2). Tentukan panjang proyeksi vektor AB pada BC
18. Menyelesaikan perkalian 2 vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
1. Diketahui dua vektor a dan b seperti gambar di bawah,
Tentukanlah nilai a . b
PEMBAHASAN:Karena kedua pangkal vektor belum berimpit, maka kedua vektor digambar menjadi
PEMBAHASAN:Karena kedua pangkal vektor belum berimpit, maka kedua vektor digambar menjadi

2. Jika diketahui dua vektor a dan b dimana a = 6 cm dan b = 4 cm serta berlaku ( a + b ).( a + b ) = 16. Tentukanlah nilai a . b
Jawab
3. Diketahui tiga titik A(4, -1, 2), B(5, 2, 5) dan C(-3, 4, 0). Tentukanlah nilai AB . AC
PEMBAHASAN:


19. Menyelesaikan 3 vektor membentuk sesitiga (lancip, tumpul, siku-siku, siku-siku yang sama kaki, siku-siku yang tidak sama kaki, sama kaki, sama sisi) dalam ruang berdimensi dua (bidang) dan dalam berdimensi tiga
Contoh soal
=
1. Diketahui segitiga ABC dengan titik
A(2, 1, 5), B(-2, 3, 3), C(1, 0, 3) besar sudut BAC = .... ?
PEMBAHASAN :
Diketahui :
A(2, 1, 5)
B(-2, 3, 3)
C(1, 0, 3)
Ditanyakan :
Sudut BAC = .... ?
Jawab :
Sudut BAC adalah sudut antara vektor AB dan AC
AB = b - a
AB = (-2, 3, 3) - (2, 1, 5)
AB = (-4, 2, -2)
|AB| = √((-4)² + 2² + (-2)²)
|AB| = √(16 + 4 + 4)
|AB| = √(24)
|AB| = 2 √6
AC = c - a
AC = (1, 0, 3) - (2, 1, 5)
AC = (-1, -1, -2)
|AC| = √((-1)² + (-1)² + (-2)²)
|AC| = √(1 + 1 + 4)
|AC| = √6
AB . AC = (-4, 2, -2) . (-1, -1, -2)
AB . AC = -4(-1) + 2(-1) + (-2)(-2)
AB . AC = 4 - 2 + 4
AB . AC = 6
AB . AC = |AB| . |AC| . cos A
6 = 2√6 . √6 cos A
6 = 12 cos A
cos A = 6/12
cos A = 1/2
cos A = cos 60°
A = 60°
Jadi sudut BAC = 60°
2.
. 

20. Menyelesaikan nilai mutlak selisih/penjumlahan 2 vektor dalam ruang berdimensi dua (bidang) dan berdimensi tiga
Contoh soal
=
Jika panjang vektor a = 4, dan panjang vektor b = 6, dan panjang vektor a+b = 8, hasil dari panjang vektor a-b =
PEMBAHASAN:





















No comments:
Post a Comment